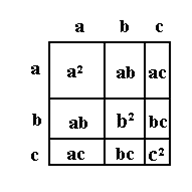
Квадрат суми трьох виразів
(а + b + с)2 = а2 + b2 + с2+ + 2аb + 2ас + 2bс
квадрат суми трьох виразів дорівнює квадрат першого виразу додати квадрат другого виразу додати квадрат третього виразу додати подвоєний добуток першого та другого виразу додати подвоєний добуток першого та третього виразу додати подвоєний добуток другого та третього виразу.
Геометричний зміст формули квадрата тричлена
Площа квадрата зі сторонами а+b+с дорівнює сумі площ квадратів зі сторонами a, b, с і двох прямокутників зі сторонами а і b, двох прямокутників зі сторонами b і с і двох прямокутників зі сторонами а і с:
(a+b+c)2=a2+b2+c2+ab+ab+bc+bc+ac+ac=a2+b2+c2+2ab+2bc+2ac.
Різниця квадратів двох чисел
(a−b)(a+b)=a2−b2
Читається :
різниця квадратів двох виразів дорівнює добутку різниці та суми цих виразів.
Геометричний зміст формули різниці квадратів
Площа прямокутника зі сторонами (а+b) і (а-b) дорівнює різниці площ квадратів зі сторонами а і b.
S-площа квадрата зі стороною a. По малюнку бачимо S=S1+S2 таким чином, маємо :
a2=b2+(a-b)2+2(a-b)b
a2-b2=(a-b)(a-b+2b)
Отже , a2-b2=(a-b)(a+b).
Куб суми двох виразів
Читається :
куб суми двох виразів дорівнює куб першого виразу додати потроєний добуток квадрата першого та другого виразу додати потроєний добуток першого та квадрата другого виразу, додати куб другого виразу.
Геометричний зміст
Виходячи з малюнка маємо :
(a+b)³=(a+b)²(a+b)=(a²+2ab+b²)(a+b)=
=a3+a2b+2a2b+2ab2+b2a+b3=a³+3a²b+3ab²+b³
= a³+3a²b+3ab²+b³
Джерело : http://www.mathematische-basteleien.de/binomi.htm .